Gnomos, calzoncillos y… correlación

Por Germán Tessmer y  Luciano Jara Musuruna

Los gnomos de South Park

Era otro día, estábamos haciendo zapping, cuando al pasar dimos con un capítulo de la serie animada South Park. Como en días de flojera anteriores ya habíamos encontrado algunas teorías económicas mezcladas dentro de los chistes –sobre todo en los aparentemente sin sentido-, decidimos ponernos en modo economista, explicar a nuestros convivientes que ahora estábamos trabajando, y pasamos a ver de forma exhaustiva el episodio que estaba comenzando titulado “Gnomos”.

El programa nos recordó algunas publicaciones de sitios de economía y finanzas que, con un estilo parecido al de esta sección, utilizaban dicho capítulo como ejemplo para referirse a algunas discusiones de política económica, y también al comportamiento de los microemprendedores. Sin embargo, en este artículo lo usaremos para explicar correlaciones.

En el episodio en cuestión, los cuatro niños que hacen de personajes principales de la serie son obligados a realizar un ensayo sobre actualidad, junto con Tweek, un niño raro y nervioso. Sin embargo, este chico sugiere que la hagan acerca de los misteriosos gnomos que se roban sus calzoncillos. En la serie, se muestra que el motivo de este robo es el de generar beneficios económicos, como dice uno de los gnomos “robar calzoncillos, gran negocio”.

Estos enanos de manera amistosa les revelan a los 4 niños el plan de negocios detrás de la operación, que consiste en 3 fases:

• Fase 1: robar calzoncillos
• Fase 2: ?
• Fase 3: Ganancias

Justamente a este punto queríamos llegar. El chiste que se puede interpretar de varias formas, a nosotros nos sirve de puntapié para explicar las mediciones y correlaciones.

Calzoncillos como índice

La venta de ropa interior masculina es de hecho un conocido indicador del ciclo económico, que incluso es consultado por economistas de la talla de Alan Greenspan, ex presidente de la reserva federal de EEUU (véase Men’s Underwear Index en Wikipedia).

¿A qué se debe esto? Si bien se trata de un producto cuyas ventas se mantienen relativamente estables la mayoría del tiempo, al producirse una crisis económica de importancia sufren una caída muy fuerte: de ahí la importancia de este indicador. Lo anterior significa que cuando uno no dispone de ingresos, decide ajustar aquello que no se ve, por así decirlo. De la misma manera, cuando comienza una recuperación crecen las ventas de calzoncillos.

Este indicador tiene la ventaja de que es muy sencillo de construir, por lo tanto, los datos del Índice de Calzoncillos suelen estar disponible mucho antes que las principales variables económicas, que requieren mayor elaboración (ni que hablar del PBI). Esta ventaja, es lo que realmente le otorga importancia al indicador. Las mediciones de otras variables llegaran algunos meses después de que la recuperación haya comenzado.  Inclusive, algunas comenzaran a repuntar unos meses más tarde. Las ventas de calzoncillos, reaccionan y se miden rápido. Podríamos decir que miden el minuto a minuto de la economía.

Calzoncillos por cemento

En Argentina, varios economistas han manifestado en los últimos días que se observan algunas señales de recuperación económica. Indicadores como los despachos de cemento, o las ventas de algunos artículos muestran una mejoría, pero la realidad es que esta supuesta recuperación (o al menos, desaceleración de la caída), es muy difícil de confirmar. De hecho, los últimos datos de actividad disponibles siguen marcando mermas en términos interanuales.

Justamente, la dificultad radica en la falta de datos económicos en tiempo real como para poder realizar dicha evaluación. Por ejemplo, en el caso de la actividad industrial, a la fecha de redacción de éste informe, la última medición disponibles del Estimador Mensual Industrial data de fines de enero. Por lo que sí, en una situación hipotética, a partir de febrero se produce una recuperación, habrá que esperar recién hasta fines de marzo para poder observarlo.

Esto pone en evidencia de contar con distintos indicadores que puedan ser rápidamente calculados y analizados para adelantar conclusiones. Y no es importante solo para el sector público, también el sector privado. Imagínese a un inversor privado que logre anticipar una recuperación económica podría, por ende, adelantar decisiones y sacar ventaja a sus competidores -el ejemplo se vuelve extremo en el mundo bursátil-. El índice de calzoncillos brinda información muy parcial, eso no está en discusión, pero tiene la ventaja de la inmediatez.

Ahora, si bien el dato de color puede resultar interesante, no es el único tema que se buscaba tratar en este artículo. Volvamos nuevamente al capítulo de la serie animada: ¿por qué roban calzoncillos los gnomos? Al parecer, porque interpretaron los datos de forma errónea.

Imaginemos a unos de los gnomos detrás de un monitor observando los datos del desempeño de la economía norteamericana ¿Qué es lo que observaría? Que cada vez que crecen las ventas de calzoncillos, la economía se encuentra en las puertas de una recuperación económica. O de forma inversa -más claro aún- que justo antes de que empiecen a caer las ventas de todo (lo que luego llevara a una reducción en la producción), caen las ventas de calzoncillos. Así, asumen que más calzoncillos generan un mejor desempeño de la economía, solamente porque hay una correlación entre ambas variables.

¿Causalidad?

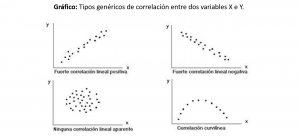
Aquí era donde queríamos llegar, el problema es que los gnomos no logran diferenciar una simple correlación entre dos variables de una relación de causalidad entre las mismas. Dos series o indicadores se encuentran correlacionadas cuando varían en forma similar (o negativamente correlacionadas, si varían en forma inversa). Pero bajo ningún punto de vista eso implica que necesariamente una sea causa de la otra. Esta distinción es fundamental, y puede llevar a muchas malas interpretaciones. Es que a diario nos encontramos con este tipo de afirmaciones. De hecho, muchas veces el común de la gente o incluso periodistas profesionales, asumen que cualquier serie correlacionada puede presentarse como evidencia de algún tipo de argumento que ellos defienden.

En vista de llevar el argumento al absurdo, se debe tener en cuenta que algunas series correlacionadas no tienen el más mínimo sentido. Por ejemplo, el gráfico siguiente muestra una correlación muy ajustada del número de personas que se ahogaron al caer en una piscina en EEUU contra la cantidad de apariciones de Nicolas Cage en películas por año (para ver más ejemplos de correlaciones espurias, se puede visitar el siguiente link: http://www.tylervigen.com/spurious-correlations). Nótese también que la correlación entre dos variables hace referencia al grado a la variabilidad asociada de cada una, más que al nivel que alcanzan en la medición cada una de éstas.

Lo que es más importante aún, es que cuando hay dos series correlacionadas, en muchos casos es difícil establecer que variable genera la otras, es decir cuál causa a cuál. Por ejemplo, si examinamos los datos de crímenes cometidos y policías asignados en cada barrio, es posible que veamos que se cometen más crímenes donde se asignan más policías. ¿Puede esto ser tomado como una evidencia en contra de la efectividad de la policía? Seguramente no. Por el contrario, lo más probable es que el gobierno decida enviar más policías donde se cometen más crímenes.

Hace poco, una noticia citaba en un estudio según el cual la gente delgada tiende a consumir más chocolate que quienes tienen sobrepeso. No se emocionen, probablemente no sea que el chocolate adelgace, sino que quienes ya se encuentran obesos traten de evitarlo. En definitiva, tenemos varias opciones, puede ser que la variable A cause B, o que la variable B cause A, o hasta que exista un variable C que podría ser una variable intermedia o la causa tanto de A como de B, y por ultimo también tenemos el azar (que muchas veces es muy difícil de descartar).

Cuando se está llevando a cabo una investigación económica seria para estimar los efectos de una determinada medida de política, estamos ante un problema de inferencia causal. Es decir, queremos evaluar el efecto del programa sobre los resultados. Es indispensable entonces tratar de aislar los efectos, a los fines de establecer en qué medida solo ese programa ha contribuido a cambiar un resultado. Existen varias técnicas, pero lo fundamental es que, si se quiere testear, por ejemplo, si los policías reducen el crimen, debe analizarse una asignación de policías que no esté correlacionada con los niveles de criminalidad, porque si no arribaríamos un resultado altamente sesgado.

Otro ejemplo en economía, muy utilizado por los medios de comunicación, tiene que ver con las explicaciones más comunes acerca de la inflación. En general, una de ellas indica que la misma es causada por los cambios en la cantidad de dinero en la economía. Al incrementar la oferta monetaria, aumenta el nivel de precios; afirman. Es más, algunos manuales de economía comienzan de hecho mostrando una fuerte correlación entre la oferta de dinero y la tasa de inflación. Pero, ¿es esto evidencia irrefutable? No necesariamente, recuerde como un mantra que:

“Correlación no implica causalidad”

Otras teorías, denominadas de dinero endógeno, de hecho sostienen que es la inflación lo que genera un aumento en la oferta de dinero, ya que influye en la cantidad nominal de préstamos otorgado por los bancos[1].

En síntesis, de este capítulo delirante de la serie animada, podemos extraer dos lecciones muy importantes para el análisis económico. En primer lugar, los indicadores que pueden medirse rápidamente son valiosos. En segundo término, que dos series muestren un comportamiento similar, no implica que estén causalmente relacionadas.

[1] Por supuesto, que esta otra teoría sea cierta no invalida el hecho de que la primera puede serlo también. Y en particular, la teoría de dinero endógeno pierde validez cuando el incremento en la oferta de dinero se deriva de una mayor base monetaria y no de un mayor multiplicador.